“Do you want to buy a car?” If this is the situation, how would you choose a car? Assume that you need a car with better features. Will you go on testing or checking all the car models in the world and then buy it? My answer would be no. I shall separate out or decrease my domain of choice to two companies(say x and y). From x and y, I will choose the top end or a car with the desired features. What have I done here?

I have set some rules or conditions to decrease my domain of choice. Again after restricting to two models, based on the features, we concluded our selection. Our Greedy technique works in the same way. Let’s see how. 

Prerequisite zone:

Assume that we have to travel from place A to place B. We can go by walk, bike, car, train or by flight. Now, I have a constraint that we should reach the destination in 10 hrs (assuming a larger distance). From the possible means of transport, train and flight can satisfy the constraint. So, train and flight are our feasible solutions. 

Again, my travel should be in such a way that, the traveling cost should be minimum. In this case, the train is our only means which is our optimized solution.

Feasible solution: A set of solutions that satisfies the constraint (or condition) on the problem.

Optimal solution: A solution that satisfies the goal of the problem. Hence the problem is also called an optimization problem.

In the above problem, time is a constraint and the minimum cost is the goal of the problem. Also, since the desired solution is “minimum of all” (minimum of all the expenses), it is also called a minimization problem. If the goal of the problem is “maximum cost or luxury” it would be a maximization problem.

Not all feasible solutions are optimal. But the optimal solution is always a feasible solution. For every problem, there exists only one optimal solution.

Greedy method or Greedy Technique:

It is an algorithm (more precisely a technique) that solves a problem by finding an optimal solution at every step as it attempts to find the optimal solution for the overall problem. In simple terms, it finds the optimal solution for each subproblem in its path to find the optimal solution to the bigger problem. It doesn’t verify if the solution is optimal for the overall problem. (Definition seems recursive!?)

From our car selection, we are narrowing the domain of selection to two companies and selecting from them. But is it the best car when the bigger picture (cars around the world)? No. This is a greedy approach. We are selecting from the subproblem (the two companies) and in the perspective that it is the best car, with respect to our constraint or rule.

Does this technique work everywhere? No. It works in some problems such as Huffman coding, Fractional Knapsack problem, etc. Where it doesn’t work? Let’s see an example.

We require a maximum sum from the given tree below.

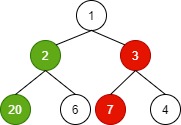
From the above figure, if we follow the greedy method (marked red) from the root (1), the result will be 8. Why? From one, the next maximum value is 3 out of 2 and 3. And the next will be 7 out of 7 and 4. The final solution is 11 in the Greedy approach.

But the maximum value can b achieved if 2 selected from 2 and 3. The total would have been 23 which is the maximum from the tree. Hence, the greedy do not satisfy the goal. This is the limitation of the Greedy technique.

References and Recommendations:

• Dijkstra’s Algorithm
• Prim’s Algorithm
• Huffman’s Encoding Algorithm
• Dynamic Programming
• Fractional Knapsack problem
• Kruskal’s Algorithm