Reading Time | ~6min

Although not very efficient, it is among the very first sorting techniques that a computer programmer learns. In this post, I’ll be explaining this algorithm and analysing it through the lens of time complexity.

Before moving on to the algorithm, let me explain the meaning of performing a sort. Let’s assume that you have been given a handful of chocolates. All of them are of different sizes, and since you aren’t feeling particularly hungry, you decide to eat the smallest one. To find the smallest, you apply a mental heuristic, probably checking the weight or the thickness and size of the wrapping. In the end, most people will manage to find the smallest chocolate piece very quickly, but if we were to give the same problem to a computer, there is very little chance that the computer would find the smallest chocolate piece on its own.

For this very reason, we end up writing sorting algorithms to “sort” items using a computer (since a computer is not very clever). Items can be letters, database records, or even chocolates. Bubble sort is an algorithm which can be used for sorting items. We’ll sort integers and characters using it.

Algorithm

Bubble Sort works by checking every pair of adjacent elements in the array. The algorithm also works for a vector or a list, so I’ll use the term array to refer to all three. It is named so because after every pass through the array of elements/keys, the largest (in case of sorting in ascending order) elements “bubble-up” to the end of the array. If there are n elements in the array, then in the worst case, the algorithm makes n-1 passes, where a single pass refers to the algorithm checking all unsorted elements of the array once.

Algorithm: BubbleSort(A, n)
Given an array A having n elements, this algorithm sorts the array in ascending order. ‘last’ stores the index/position of the last sorted element. The variable ‘exchanges’ counts the number of times elements have been swapped in a pass. Indices of the array range from 0 to n-1.

1. Repeat through step 4 n-1 times.
2. Repeat step 3 for elements in unsorted array.
3. If current element is greater than the next element, then exchange elements and increment ‘exchanges’
4. If no exchanges were made, i.e. ‘exchanges=0’, then return.
   Otherwise reduce the value of ‘last’ by one.

Implementation

The following code shows a bubble sort implementation in C99.

/*
    Program to perform bubble sort on a character array.
    COMPILER: gcc 10.1.0 (options='-std=99')    
*/
        
#include‹stdio.h›
#include‹string.h›
        
void displayArray(char*);
/*Procedure to display elements in the array*/
void bubbleSort(char*);
/*Procedure to sort elements of the array.*/
        
int main(void){
    char array[] = {'K', 'B', 'D','U', 'P'};
    printf("Original Array\n");
    displayArray(array);
              
    bubbleSort(array);
        
    printf("Sorted Array\n");
    displayArray(array);
    return 0;
}
        
void displayArray(char* a){
    for(int i = 0; a[i] != '\0'; i++)
        printf("%c ", a[i]);
    printf("\b \n");
    /*To remove the trailing whitespace.*/
}
        
void bubbleSort(char* a){
    int lastIndex = strlen(a);
    int passes = lastIndex;
    int exchanges;
    for(int i = 0; i < passes; i++){
        exchanges = 0;
            for(int j = 0; j < lastIndex-1; j++){
                 if(a[j] > a[j+1]){
                     int temp = a[j];
                     a[j] = a[j+1];
                     a[j+1] = temp;
                     exchanges++;
                 }
             }
             if(exchanges == 0)
                  return;
             else
                  lastIndex -= 1;
     }
}

Analysis

Before you read this section, you may need to brush-up your knowledge of notations used in analysis of algorithms. I have written about this in a previous post.

Worst-case Time Complexity

In a bubble sort, the worst case to sort the array in ascending order is when all the elements are already arranged in descending order. The basic operation cop is the comparison between adjacent elements. Assume the array is as follows:

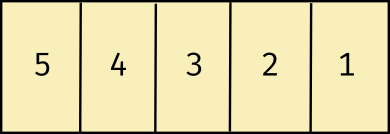
Initially, n = 5, last = 4 and exchanges = 0. We have taken arrays as zero indexed, i.e. element 5 is at index 0, element 4 is at index 1 and so on. After the first pass, the element at index 4 (last position) will be 5. Generalizing, in an array with n elements, in the first pass, n-1 comparisons will be made. The comparisons are as follows:

1. 5>4? (Yes; ∴ swap 5 and 4).
2. 5>3? (Yes; ∴ swap 5 and 3).
3. 5>2? (Yes; ∴ swap 5 and 2).
4. 5>1? (Yes; ∴ swap 5 and 1).

Thus, n-1 = 4 comparisons. Now, since 5 is in its correct spot, we don’t need to perform another comparison with 5 in the remaining passes. As a result, in the next pass, we don’t consider the index of 5 during comparison. Similarly, for each subsequent pass, the size of the unsorted array decreases, since sorted elements essential “bubble up” or “sink” to the end of the array. For this reason, the bubble sort is also called as a sink sort, since heavier weighted elements reach the end of the array after each pass. After the first pass, the arrangement of elements is shown below.

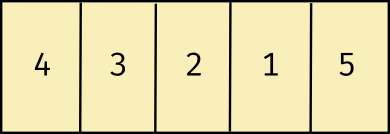
In the second pass, n-2 comparisons will be made. These are as follows:

1. 4>3? (Yes; ∴ swap 4 and 3).
2. 4>2? (Yes; ∴ swap 4 and 2).
3. 4>1? (Yes; ∴ swap 4 and 1).

Thus generalizing for every subsequent pass, the number of times cop gets executed is given by the sum
T(n) ≈ (n-1) + (n-2) + (n-3) + (n-4) + ...+ 3 + 2 + 1
This is equal to {(n-1) * ((n-1) + 1)}/2 = ((n-1)*n)/2
Thus the bubble sort algorithm has a worst case complexity of order n2. This is represented as Ο(n2), and read as “Big-Oh of n-squared”.

Best-case Time Complexity

We can observe the best case complexity when all the elements in the array are already sorted. In such a situation, at least one pass needs to be performed, at the end of which the algorithm concludes that the array is sorted, since the variable ‘exchanges’ will not have changed in the end. An example is given below.

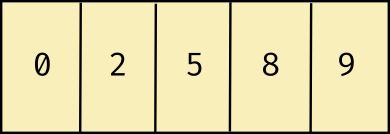
In the above state, comparison between adjacent pairs will be performed until the last comparison between elements 8 and 9 is performed. After this, if the variable ‘exchanges’ is equal to zero, it implies that the array is sorted.

In this case the time complexity is of order n since it is the least number of times the basic operation is performed. In an array containing n elements, the best case time complexity is proportional to the number of elements n. Thus the best case time complexity is represented as Ω(n), read as “Big-Omega of n”.

Average-case Time Complexity

The average case complexity of bubble sort also of order n2. Although I couldn’t find many sources verifying the book by Tremblay and Sorenson mentions this.

Among the three cases, the worst-case complexity is of prime importance in many applications.

Enfin

Although bubble sort is rarely used anywhere, I intended to explain a basic sorting algorithm before moving on to complex ones. Stay tuned for more !

Introduction to AWS

by Tharun Buddigina February 24, 2023

How to create your own programming language?

by Suraj Naranatt August 17, 2022

Password Security – First Line of Defense against Cyber-Attacks

by Guest_Techprodezza October 12, 2021