Have you ever thought of how your data on Internet is secured? When you send a photo on any platform, it will be compressed, encrypted and transmitted. The image should be transmitted without any loss in pixels or data. So, several algorithms play a major role in these operations. One such algorithm is Huffman coding algorithm.
Prerequisite: What is a prefix code? It is defined as a bit sequence that is assigned to a character and is not the part of any code assigned to other character. Confused? Let’s take an example!
| Character | Code |
| A | 00 |
| B | 01 |
| C | 100 |
| D | 101 |
| E | 11 |
Observe from Table 1; If you consider A its code is ’00’. It is unique and is not a part of any other code assigned to characters B, C, D or E. Similarly, it is applicable for all the characters. Hence it is a Prefix code or Prefix- free code. Both are one and the same, if not bothered about how the names are assigned 😁. Now let’s get into our actual algorithm!!
Let’s consider we have a string BBCDDDEAEEBAACC that is to be transmitted.
If we use ASCII encoding, it takes 8 bits (4 bits=1 byte) for each character. Length of our string is 15. So, if message has to be sent, we require 15*8= 120 bits. We should compress the cost of sending message. Let us see if we will be able to accomplish with Huffman’s Algorithm.
Algorithm:
- Make a table that has has columns: characters, frequency of characters and code as in Table 2. Bits required is optional.
- Arrange the characters in ascending order of their frequencies. Since every character has the same frequency in our string, arrangement can be in any order. We took here as A, B, C, D, E.
- On the top of every character, mark respective frequencies as in Fig 1.1.
- Now, following the Optimal Merge Pattern to construct a Tree.
- Connect the two minimum frequencies. Here 3 , 3 of A and B makes 6 as shown in Fig 1.2.
- Now we have 6 (A & B), 3 (C), 3 (D), 3 (E) on our list as shown in Fig 1.2.
- From our numbers, on connecting 3 (C) and 3 (D) gives the minimum external sum than any other combination.
- Continue step 7 till all are under a single root as in Fig 1.5
- Now mark the lines connecting nodes as 0 and 1. They are marked in such a way that the line joining left node gets 0 and to the one connecting right gets 1. This is also shown in the Fig 1.5.
- From the root node (here 15), make the code following the path from the root to that particular character. Let’s take D here. Following the path from root node to D gives 101. Similarly, we will get the codes for all the characters as in Table 2.
- Replace the characters in the string with the codes obtained. Here you will get ” 0101100101101101110011001111010000100 “. This is your required encoding.
- Stop.
Fig 1.1 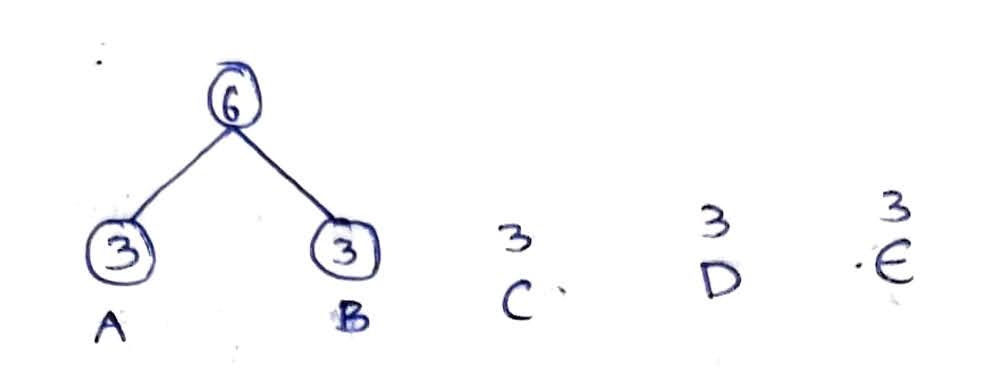
Fig 1.2 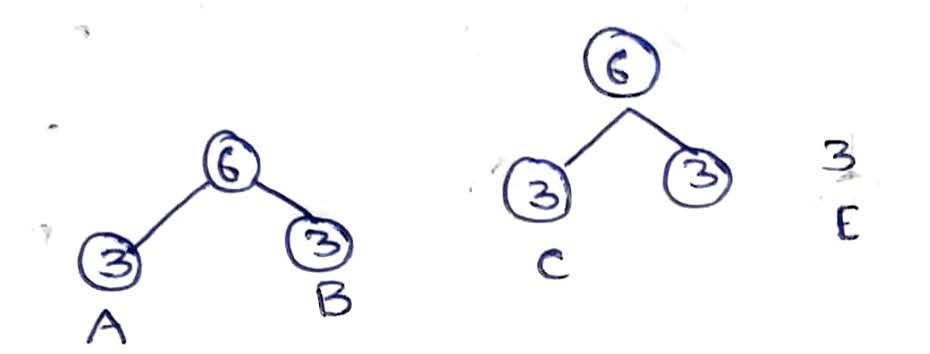
Fig 1.3 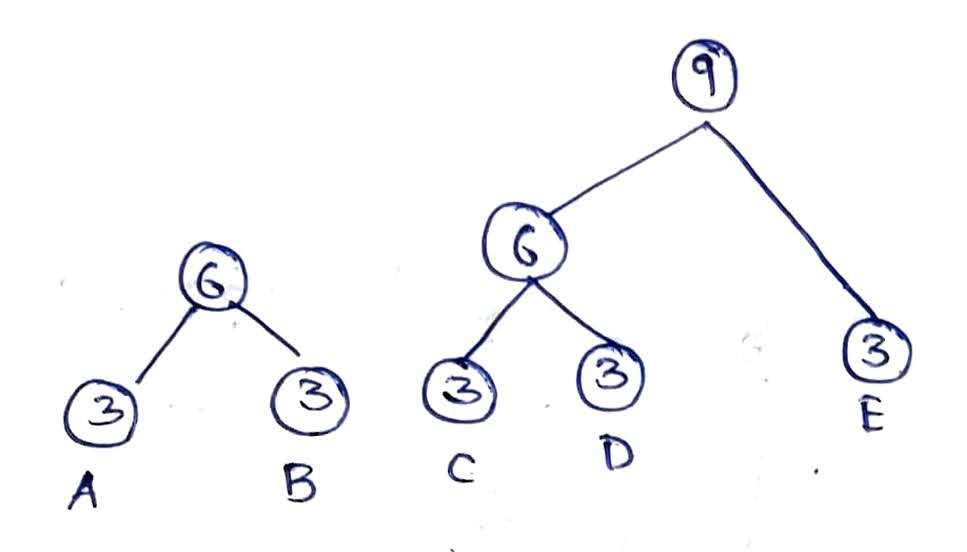
Fig 1.4 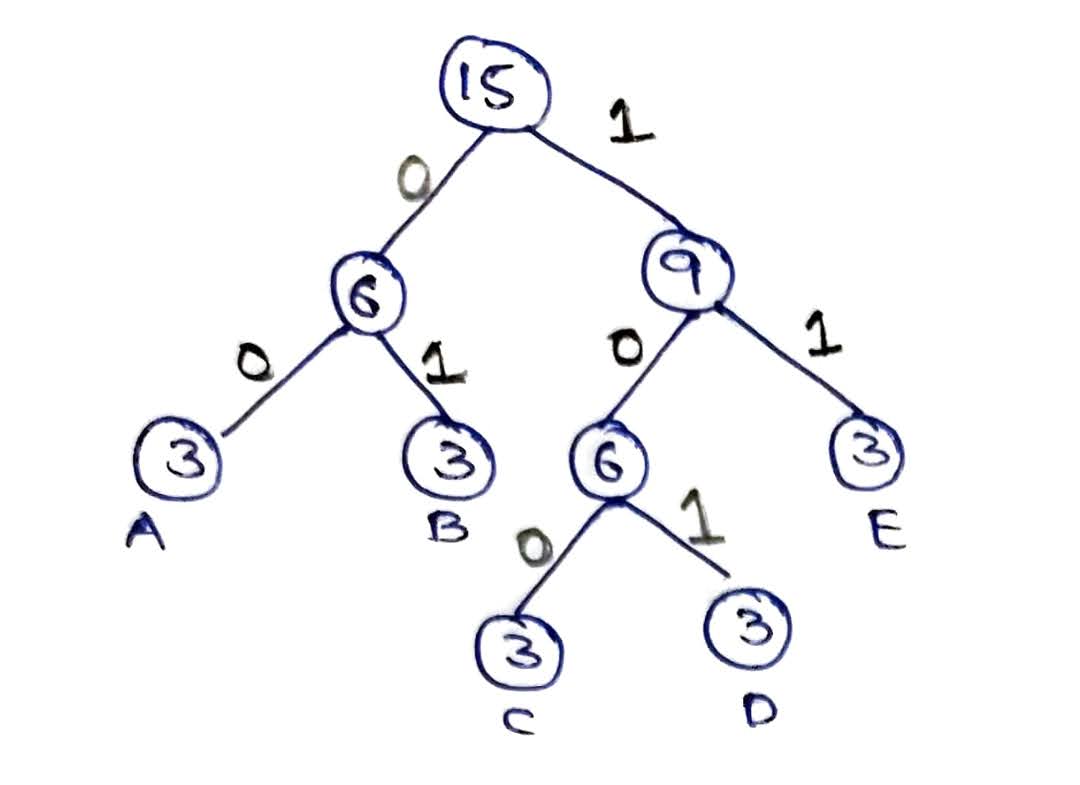
Fig 1.5
| Character | Frequency | Code assigned | Bits required |
| A | 3 | 00 | 3*2=6 |
| B | 3 | 01 | 3*2=6 |
| C | 3 | 100 | 3*3=9 |
| D | 3 | 101 | 3*3=9 |
| E | 3 | 11 | 3*2=6 |
From the Table 2, we came to know that the total number of bits required to transmit the message is 36. When we send the message in encoded format, we have to transmit the table to refer inorder to decode the message. So, the number of bits of required to transmit the table is ( 5*8 bits (8 bits are required to represent character in ASCII) + 12 bits ( number of bits of code: 00 (2 bits); 01 (2 bits) and so on.) ) 52. It is not mandatory to send frequency column.
They sum to a total of 52 bits along with the table. If ASCII encoding is used, that would have been 120 bits which is more than double of what we got. So, hence proved that Huffman coding can be used to compress the cost of transmission. Next question is how does the decoding happen?
Decode it!!
It is not as complex as it seems. You will be given the table and the encoding. Since Huffman coding is a Prefix- free code, we can decode it without constructing the tree. 0101100101101101110011001111010000100 this is our code. Starting with first bit, we have 01 which resembles B from the table. Also the same code (of B) is not a prefix to the code assigned to any other character. So what we get the initial code is our original message. And similarly, from fifth bit it is 100 that resembles C from the table and so on. Through this procedure we can decode the message 😉.
If still you wish to construct a tree, then we know that when we encounter zero that moves to the left of the node and to the right if one. So, we construct a tree considering the given codes for characters and obviously the characters will be as leaf nodes. Suppose 01 resembles B and in tree it goes to the left of the root and right of the next node. Similarly, we can figure out the complete tree. But this is time consuming than the initial method. This is all about Huffman coding algorithm. This is just an explanation to the algorithm. The condition if it is secured or not is a different domain. There are other methods to encode and encrypt data.
Note:
Huffman coding need not to be unique. It changes according to the convention you take while marking 0s and 1s. Also depends when the multiple characters have same frequencies or the identical external path length and the arrangement of characters of identical frequencies. So, the solutions provided here are just one way of encoding.
Practice for more understanding:
- TECHPRODEZZA; encoded string: 1110001101011000111011001010000010010100
- AABDDECCA; encoded string: 1111001001000110110111
Neologism:
- Prefix code: It is defined as a bit sequence that is assigned to a character and is not the part of any code assigned to other character.
- Optimal Merge pattern: It corresponds to form a binary tree with two nodes such that the result node should have minimum weighted external path length. This follows Greedy algorithm. Quiet understandable from the example!
- ASCII: American Standard Code for Information Interchange
- ASCII decimal values: A-Z: 65-90; a-z: 97-122; 0-9: 48-57
References and Recommendations:
- Greedy Method
- ASCII Values
- Cryptography: Various encrypting types.
5 thoughts on “Huffman’s Coding Algorithm”