I am pretty sure that we all have seen trees, at least in cartoons! Let us fill a questionnaire regarding the details of a tree.
Which is the most vital part of a tree? Or the other way, where does a tree start growing? Root, obviously.
What does a tree have connecting to the roots, directly to the trunk? Branches!
What does a tree have at the end of the branches? Leaves!
If we answered these questions, we have understood the basics of a tree in Data Structures.
Not clear how? Let’s grow.
Basics of a tree:
A tree is a non-linear data structure used to represent data that is in the hierarchical form. For example, commonly called a Family tree. The below image shows a sample of the hierarchy of a family.

Terminology of Trees:
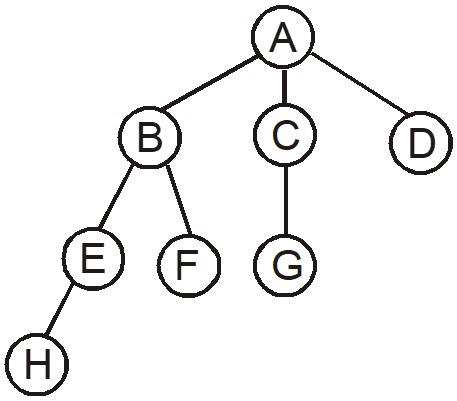
We will discuss the terms with reference to the above figure. For more understanding, read synchronously.
Each entity of a tree is known as a node. The above tree has eight nodes.
Root: The topmost node of a tree is known as a root. A is the root.
Parent: Any node except the root node has the edge upward known as the parent.
Child: The node that is connected downward of the edge of a given upward node is called its child.
From the figure, B is the parent of E and F where E and F are known as children or child nodes. Similarly, A is the parent or root of B, C, and D. E is the parent of child node H.
Sibling: The children of the same parent are called siblings. Here B, C, and D are siblings; E and F are siblings, etc.
Leaf node: The node that doesn’t have any child nodes is called a leaf node. H, F, G, and D are leaf nodes.
Descendants: The nodes which are reachable from a particular node are known as descendants of that node. For instance, E, F, and H are descendants of B as they are reachable through B.
Subtree: It represents the descendants of a node. B and C are subtrees as they are at a downward level to A. D is not a subtree as it doesn’t have children for being called as a tree.
Traversal: The process of passing through the nodes of a tree in a specific order is known as traversal.
Visiting: Checking the value of a node.
Level: It represents the generation of a node. Assuming the root node at level 0, the children B, C, and D are at level 1, followed by their children at level 2 and so on. The above tree has three levels.
Degree of a node: The number of subtrees to a node is its degree. The degree of A is 3, B is 2, and C is 1. The degree of a leaf node will always be one.
Degree of a tree: The degree of a tree is the maximum degree of a node in the tree. For the above tree, the degree is 3 as the maximum degree of nodes is 3.
Null Tree: A tree with no nodes is called a Null Tree.
Height or Depth of a tree: The maximum level of a tree is known as the height or depth of that tree. The depth of the above tree is 3, if the root is at level 0.
In data structures, we mostly use binary trees.
Binary Trees:
A tree with the utmost two children or subtrees is called a binary tree.
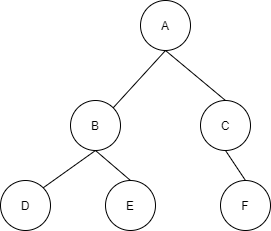
The above tree is a binary tree as it has a maximum of two children or subtrees. We shall now discuss some of the types of binary trees.
Strictly Binary Tree:
If every non-leaf nodes of a binary tree have exactly two children, then it is known as the strictly binary tree. In other words, if the degree of non-leaf nodes is always two of a binary tree then it is a strictly binary tree. A strictly binary tree of n leaves has (2n – 1) nodes.
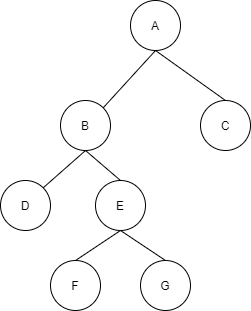
The above binary tree is strictly binary as all the non-leaf nodes have a degree of 2.
Number of leaf nodes n = 4
Number of nodes = 2n – 1 = 8 – 1 = 7
Full Binary Tree:
If all the non-leaf nodes of a binary tree have exactly two children, then it is said to be a Full Binary Tree. A full binary tree of depth d, considering root node at level 1, has 2d – 1 nodes.
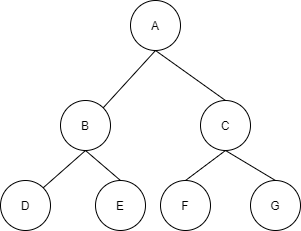
Complete Binary Tree:
A binary tree in which every level, except possibly the last, is completely filled, and all the nodes are as far left as possible. This is more understandable when represented in the form of an array.
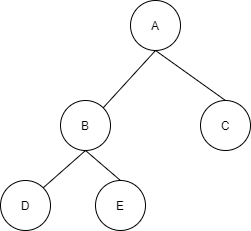
The above binary tree is complete as all the nodes are completely filled to the left.
Note: A full binary tree is always a complete binary tree and not vice-versa!
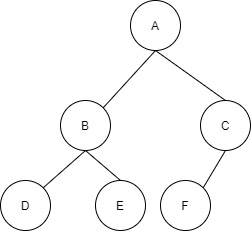
The above tree is referred to as an almost complete binary tree as the nodes aren’t completely filled but the nodes are as far left as possible.
Some formulae, incase!
Generally, the level count will be taken from 1.
Maximum number of nodes at level i is 2i-1
If the depth of a complete binary tree is d then,
Total number of nodes = 2d – 1
Number of leaf nodes = 2d-1
Number of non-leaf nodes = 2d-1 – 1
Skewed Binary Tree:
This type of binary tree has either left or right branches. If the tree has left branches it is a left-skewed binary tree and if it has right branches it is called a right-skewed binary tree.
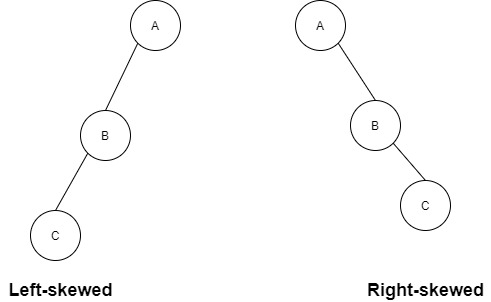
Binary Search Tree:
A binary tree in which all the nodes are arranged according to their values. The left child of the parent has lesser value than the parent and the right child has value greater than its parent.
Example:
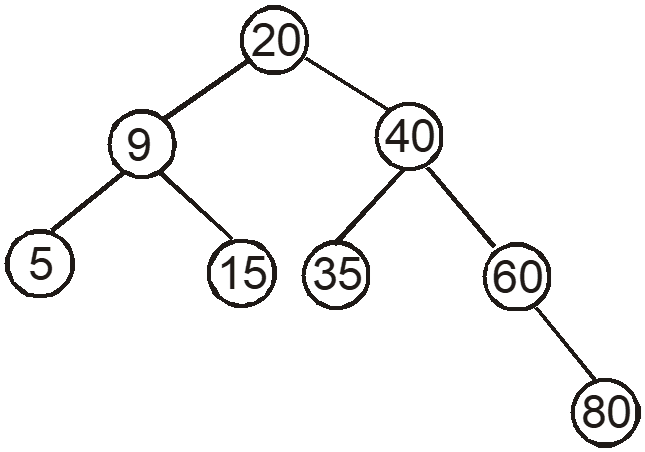
There exists other types of trees such as threaded binary tree, expression tree, etc. They will be discussed in further posts.
Applications of Binary Trees:
- Binary search Tree, a type of binary tree, used in searching algorithms.
- Spanning trees are used in routers to find the minimum paths in computer networking.
- Priority queue can be implemented using heap data structure, which is also a tree data structure.
- B -Trees and B+ Trees are used in indexing in databases.
- Hierarchical data can be stored using trees.
These are some of the applications of tree data structure and there are numerous.
The representation of trees, traversals in a tree and further topics will be discussed soon. Stay updated for more.