In the earlier posts, we have learned about trees and some its types. If not remembering, check it out! Theoretically, it is fine. But how will we represent them and make sense while actually coding them? Let’s clear our way.
Representation of Binary Trees using Arrays:
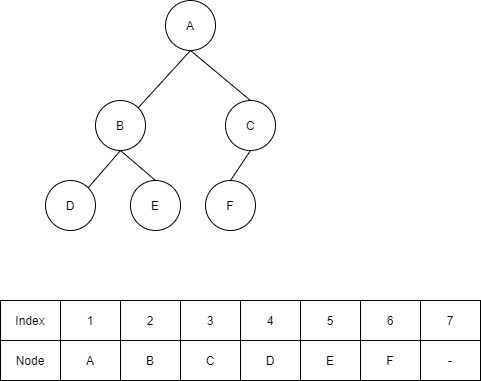
From the above figure, we can conclude that it is a complete binary tree since all the nodes are arranged as far left as possible. For more understanding, refer to the article on Trees. We can also conclude if a tree is complete or not by representing it in the form of an array.
Let’s take an array of size 2d – 1 where d is the depth of the tree. From the above tree, d=3. We represent the indices of the array, here, starting from 1 for clear understanding. But while implementing it in a programming language, we start with 0.
We will fill the array following a level order traversal. In simple terms, starting from the root, the array is filled with the values of nodes from left to right, at each level.
At index 1, the root is filled i.e. A.
At index 2, the left child of the parent (A) is filled i.e. B.
At index 3, the right child of the parent (A) is filled i.e. C.
At index 4, the left child of the first sibling (B) is filled i.e. D.
At index 5, the right child of the first sibling (B) is filled i.e. E.
Using formulae:
Assuming the root (A here) is filled at index 1,
The left child gets filled in the index (2*i) of the array, where i is the index of the parent.
The right child gets filled in the index ((2*i) + 1) of the array.
The parent can be found using floor(i/2) where i is the index of the child in the array. The parent of E is floor(5/2) = floor(2.5) = 2. B is at the index 2. It is the parent of node E.
These formulae apply to all the parent nodes and child nodes.
Now, C is at index 3 of the array i.e. i=3. Its left child will go to the index, (2*3), 6 of the array. The right child will go the index, ((2*3) + 1), 7 of the array. Similarly, all the nodes are filled in the array.
We can find the position of the parent node and child nodes using the above conditions or formulae. If any of the children are missing, then space is left empty in the array. Let’s get more clearer with another example.
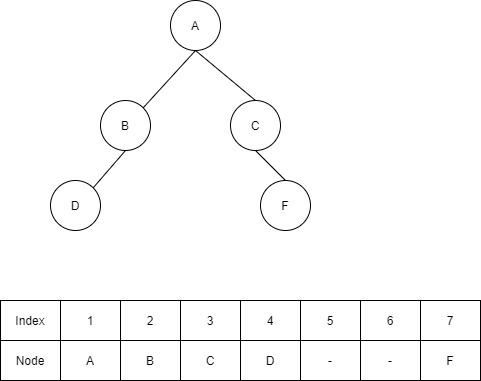
From the above example, it is clear that the right child of B and the left child of C are missing. Hence their respective indices in the array are left empty. If you observe, the gaps are left between the indices, i.e. between 4 and 7 indices. If such conditions are encountered then it is not a complete binary tree.
In the earlier case, the last index of the array is empty i.e. 7. Though it is empty and since no gaps are left between the indices, it is a complete binary tree. This is how one can find out if the binary tree is complete or not.
Snippet of representation of Binary Trees in Python
#This code represents Fig 2.
#depth of the tree=3
#Total nodes = 2^3 - 1 = 7
total_nodes = 7
tree = ['A', 'B', 'C', 'D', None, None, 'F']
#'None' is used to indicate that there exists no children or nodes.
def get_right_child(i):
# node is not null
# and the result must lie within the number of nodes for a full binary tree
if tree[i]!=None and ((2*i)+1)<=total_nodes:
return (2*i)+1
# if right child doesn't exist
return -1
def get_left_child(i):
# node is not null
# and the result must lie within the number of nodes for a full binary tree
if tree[i]!=None and (2*i)<=total_nodes:
return 2*i
# if left child doesn't exist
return -1
def get_parent(i):
if tree[i]!=None and i/2!=None:
return i//2
# if root
return -1
Notations
i → index of the array
tree → array (list in python) to represent the nodes of the tree
get_right_child → method to retrieve right child of a parent node
get_left_child → method to retrieve left child of a parent node
get_parent → method to retrieve parent of a child node.