Have you heard of ‘heap of grass’? How is it arranged? The bottom will be of larger width compared to the top, of course, the science. We can relate that to our topic, Heap data structure.

We have learned about binary trees and their representation in an array and a Linked List. This heap data structure can be considered as an application of them. If you haven’t gone through them yet, the links are provided in the “References and Recommendations” section. Now, let’s see how a heap is implemented.

Heap:

A heap is a complete binary tree. A binary tree in which every level, except possibly the last, is completely filled, and all the nodes are as far left as possible. There are two ways in which a heap can be arranged, as discussed above. They are:

Max Heap:

If the root data is greater than or equal to its descendants it is called a max heap.

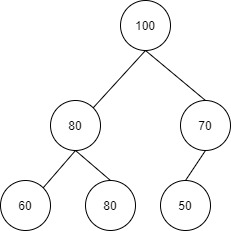
If you observe, the root node is greater than its descendants or children 80 and 70. The nodes 80 and 70 are greater than or equal to their child nodes. Hence it is a max heap.

Min Heap:

On the contrary, if the root data is less than or equal to its descendants it is called a min heap.

The root node 50 is less than its child nodes 60 and 70. The nodes 60 and 70 are less than or equal to their descendants. Hence it is a min heap. Note that the nodes should be less than or greater than one of its children.

Representation of binary tree using an array:

We have already discussed the two different representations of the binary trees. We will now use an array to denote heap.

The traversal used here is level order. It means that the elements are filled in the array or linked list from left to right at each increasing level.

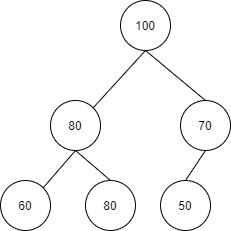
The above complete binary tree is represented as:

The root at level 1 (100) is inserted first. Then the nodes at the next level are inserted from left to right (80,70) and so on.

The left child gets filled in the index (2*i) of the array, where i is the index of the parent.

The right child gets filled in the index ((2*i) + 1) of the array.

The parent can be found using floor(i/2) where i is the index of the child in the array. The parent of 60 is floor(4/2) = floor(2) = 2. 80 is at the index 2. It is the parent of node 60.

Operations on a Heap:

We will use a max heap to perform the operations. Those can similarly be applied on a min heap with minor changes.

Insertion:

1. Insert the element in the array at the last position i.e. as a leaf node.
2. Compare the inserted element with its parent. If it is greater than its parent, swap them. This swapping continues until it reaches a node where it is less than its parent. (This is exactly the opposite for min heap)
3. Insertion is completed.

You can imagine the insertion with the tree in sync with the array.

Suppose I have to insert the element, say 60. The below images depict how the insertion is performed.

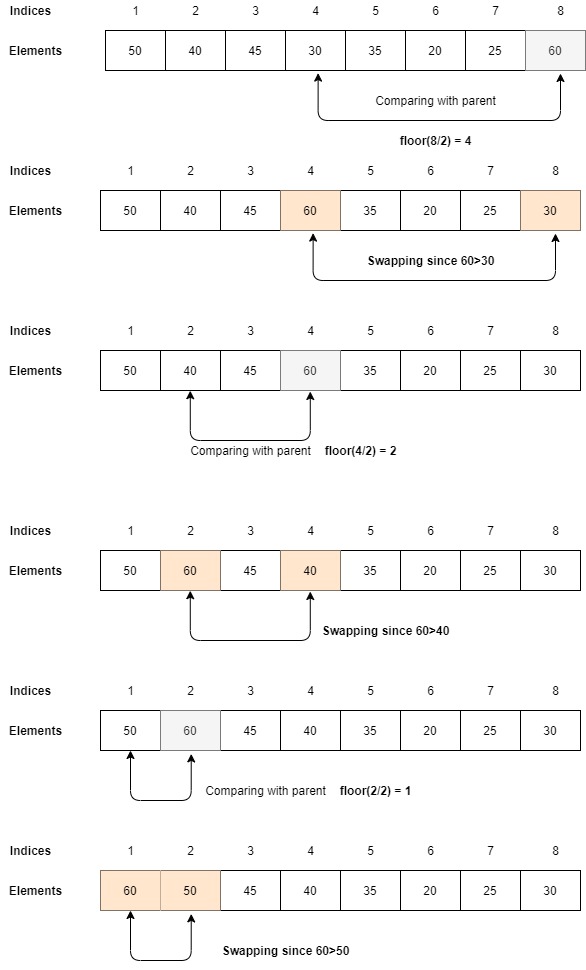
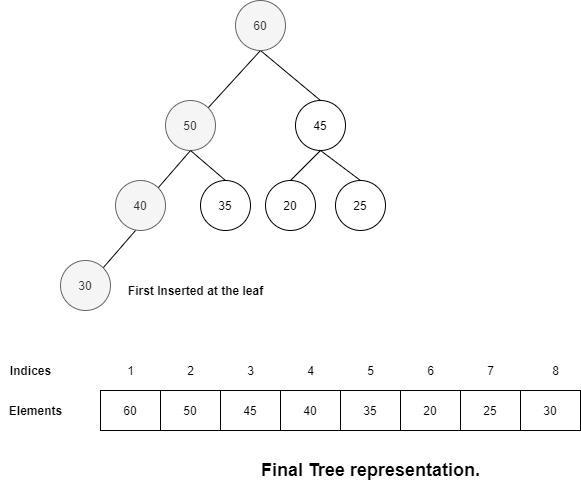
Deletion:

1. Remove the root node from the tree i.e. first element of the array.
2. Move the last element of the array to the first position. This is to achieve the property of a complete binary tree.
3. Now compare the root node (first element of the array) with its children. Replace the element with a higher value (among root and child nodes) in the position of the root node.
4. Repeat step 3 until the root node that is compared to its child nodes is greater of all.
5. Deletion is completed.

Note:

1. Only the root node can be removed from the heap. There is no meaning of heap if any of the middle nodes are removed first. If any other nodes are to be deleted other than the root then the node should be moved to the root position and perform the delete operation.
2. Whatever operation we perform on a heap, at the end it should be a complete binary tree. It can be a little hint to find if you are going on the correct path.
3. In insertion (which can also be a creation operation) the operation is performed upwards i.e. we insert the element at the last we start moving upwards.
4. In deletion the operation is performed downwards i.e. we delete the element at the top and replace it with the last node (last element of the array). Then we start moving downwards by comparing.

Time complexity:

During insertion, the best case is O(1) where the smallest of all the elements is inserted. This involves no swapping of elements. The worst or average case is O(log n) as it depends on the height of the tree. The height of the tree is denoted by log n (it is similar to merge sort). 

The maximum time taken during insertion is O(log n) which also depends on the height of the tree.

Heapify:

If we observe, we insert the elements from left to right (top to bottom w.r.t. tree) during the creation. Can’t we insert from right to left (bottom to top w.r.t. tree)? This could be a little confusing. Let’s work this out with an example.

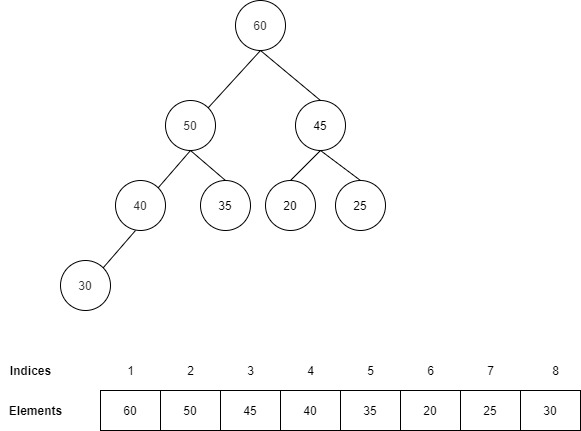
The given binary tree is a full binary tree (which is also complete) but it isn’t a max or min heap. The example is the same used for performing operations on a max heap. We will achieve max heap with the help of heapify and cross-check.

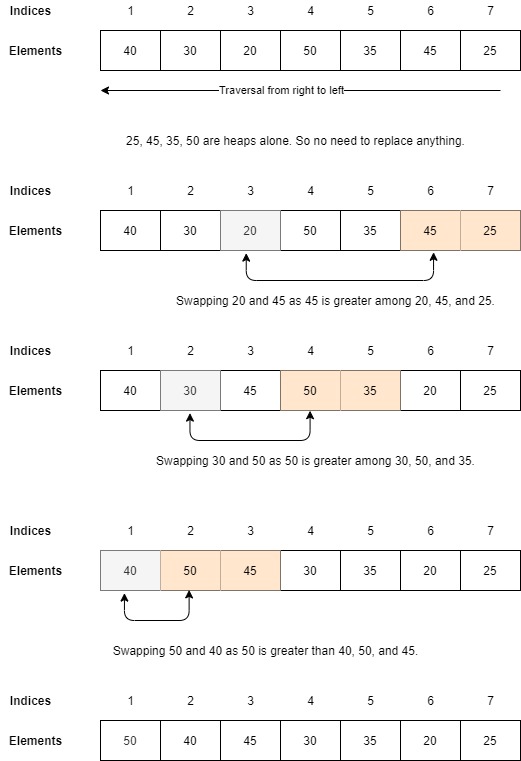
1. For the given array, we usually traverse from left to right to make it a max or min heap. We will now traverse from right to left to achieve the same.
2. All the leaf nodes are heaps alone. We should consider the second upper level of the tree (level 2 here).
3. Compare the right-most node of the tree with its children (here 20 with 45 and 25) and replace root (w.r.t. Sub-tree: 20) with the greatest among the three (20, 45, and 25). Hence 20 will be replaced by 45.
4. Continue step 3 until the parent or root node is reached i.e. 40 is reached (here)
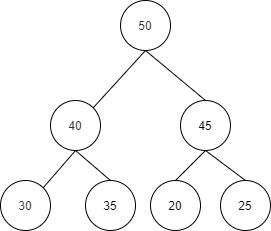
5. The tree we achieve is our required max-heap.

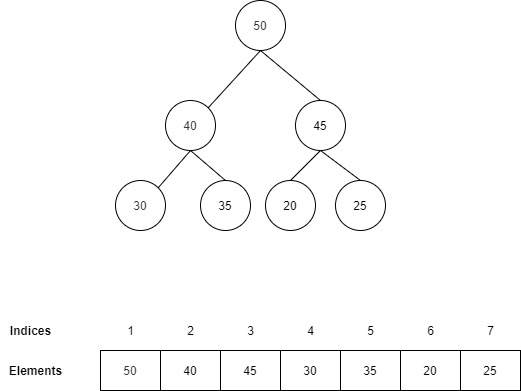
The only difference is that we do the reverse process. The heapify is similar to the deletion operation that we performed earlier.

Applications of Heap data structure:

1. Heapsort
2. Used in graphs as a priority queue
3. Priority queue

References and Recommendations:

• Heapsort
• Binary Trees using Linked List
• Implementation of Linked List
• Representation of BT using arrays
• Arrays and Linked List
• Tree Data Structure
• Doubly Linked List
• Queue