On a cold, rainy day, nothing is more welcome than a warm, sweet cup of tea(or coffee, if you like). To make a cup of this delicious liquid, a sequence of steps is followed by the person who makes it. Similarly, to solve a problem using computers, an algorithm is used. Knowledge about the meaning of the term “algorithm” is a stepping stone to understanding time and space complexity.

Algorism

The word “algorithm” has ancient roots, and was known as “algorism” during the Middle Ages. The term is actaully derived from the name of a Persian textbook author, Muḥammad ibn Mūsā al-Khwārizmī, who also wrote another book which gave the rise to the term “algebra”. Formally, an algorithm can be defined as follows:

An algorithm refers to finite series of basic operations used to solve a specific type of a problem.

It may seem very similar to a cooking recipe, but cooking recipes often include instructions such as “wait till the milk is lukewarm”. The meaning of a recipe varies depending on how much of an expert the reader is. For example, a novice may misunderstand the temperature as closer to boiling temperature. In fact, there is quite a bit of confusion regarding the exact temperature even among seasoned chefs. On the other hand, an algorithm can convey the exact sequence of steps to be followed. A sequence of steps can be said to be an algorithm, if it satisfies the following properties:

• Finiteness
• Definiteness
• Input
• Output
• Effectiveness

To explain these properties, let me give an example.

Euclid’s Algorithm

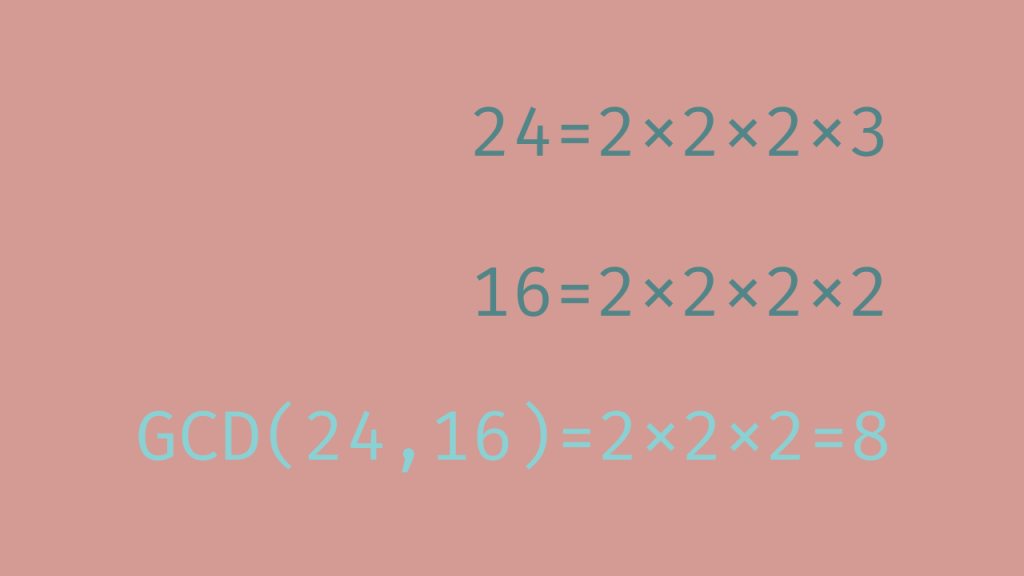
The algorithm was introduced by a famous Greek mathematician and is used to find the greatest common divisor (GCD) of two positive numbers. The algorithm is used to solve the following problem:
To find a positive integer such that it is the greatest number which exactly divides two positive integers ‘m’ and ‘n’.
When a number exactly divides another, then the remainder is zero.

The algorithm is as follows:

1. [Find the remainder]
   • Divide ‘m’ by ‘n’. Let ‘r’ be the remainder.
2. [Check ‘r’]
   • If r=0, then ‘n’ is the result. Exit.
3. [Update values]
   • m←n ; n←r and go back to step 1.

The left-arrow (←) means that the variable on the left is assigned the value on the right. Let me explain why the above sequence of steps is an algorithm.

Finiteness

The finiteness property means that an algorithm terminates in a finite number of steps. The above sequence of steps satisfies the finiteness property since in step 2, if r = 0, then the algorithm terminates, otherwise execution continues to step 3. In step 3, the value of m and n are changed, and the value of n is always reducing with each execution of step 3, until r becomes 0 or n becomes 1. The execution may also terminate when n becomes 1 because it is the greatest positive integer that divides any other positive integer in case they don’t have any common factors.

Definiteness

This property means that each step of the algorithm is unambiguous and precisely defined. Each step in the above algorithm is definite since the reader knows the exact meaning of the phrase “exactly divides m by n”.

Input

The input in the above algorithm is the set of two numbers from the set of all positive integers. A sequence of steps must have an input for it to be an algorithm. There may be one or more inputs in an algorithm.

Output

The output in Euclid’s algorithm is the greatest number which divides the two inputs exactly. A sequence of steps must also produce an output for it to be an algorithm.

Effectiveness

An algorithm is said to be effective, if the operations can be performed exactly as specified, and in a finite amount of time, using pen or paper. In Euclid’s algorithm, the division of ‘m’ by ‘n’ can be exactly performed and in a finite amount of time on paper. Even if the two numbers are really large, the result can be found using a computer too, since division is a well-defined operation.

Enfin

In summary, a sequence of steps is an algorithm if it satisfies the above properties, but the restriction of finiteness is slightly unsuitable for practical use. A sequence of steps can be formally called an algorithm in that each step can be completed in a finite amount of time, but the algorithm as a whole requires a long time to execute. An example of such an algorithm may be that which determines whether or not a game of chess can be always won by the White side if the White side makes no mistakes.

In another post, I’ll explain the concept of time complexity and how it relates to better algorithms.